Hypercube Digital Signatures

“Binary codes in the head of human in the style of pop art” by DALL-E2.
Context: a new scheme
Digital signature algorithms are a cornerstone of modern information security. The padlock in your toolbar when reading this blog post indicates that your computer has authenticated the identity of the www.sandboxaq.com server via TLS. Such authentication is ubiquitous in communication protocols throughout the internet networking stack and crucially relies on digital signatures.
Today the security of signatures and authentication depends on the hardness of factoring integers or a few related problems from number theory. Due to the quantum threat, these signatures will need to be replaced, as large fault-tolerant quantum computers will easily solve the problems that currently make them secure. After a multi-year process, the National Institute of Standards and Technology (NIST) has decided to standardize three signatures based upon novel mathematical problems that the cyber community believes quantum computers can’t solve efficiently.
Research into signatures has continued at a blistering pace in the past 7 years. So much has been discovered that NIST is about to start a new process to down-select and standardize from the latest bounty of signatures. To date, the signatures selected by NIST are either based on lattices or they are significantly slower and produce large signatures. While the lattice signatures are fast, they still do not get close in terms of sizes to quantum-vulnerable signatures.
This blogpost describes a new code-based digital signature algorithm developed by SandboxAQ that significantly improves upon previously known works. SandboxAQ will be presenting the paper introducing this signature algorithm at EUROCRYPT 2023 in Lyon this week – one of the three flagship conferences in cryptography. Papers presented at EUROCRYPT are first peer-reviewed by independent experts before being accepted to the conference. Below we give an overview of the core innovations of preceding work in addition to the new material presented in the paper.
H-SDitH: Hypercube-Syndrome Decoding in the Head
First we’ll introduce zero knowledge proofs (ZKP), and how they can be used to certify one’s identity. Then we’ll speak about multi-party computation (MPC), a privacy preserving technique, and an adaptation known as MPC-in-the-Head (MPCitH) that allows MPC to be used to generate ZKPs. After discussing the bottlenecks that derive from the computation-versus-space trade-offs for MPCitH, we present our contribution - share aggregation using hypercubes! - and explain how this improves the aforementioned trade-offs. To do this, we apply the technique to a previous scheme that achieved short signatures by combining MPCitH with the syndrome decoding (SD) problem. The details of SD and what makes it so great for cryptography are for another post, though.
Zero Knowledge Proofs
A zero knowledge proof is an interactive protocol in which a prover can convince a verifier that they know a secret without revealing anything about the secret. More formally, the prover performs a computation on a secret $x$, the result of which proves that they know $x$, but without letting anyone learn any information about $x$ whatsoever. Signatures can be thought of as a non-interactive ZKP where you are proving that you 1) know your own private key, and 2) bind this proof to a message. In information security, knowledge of your private key is a proxy for your identity. Hence, proving knowledge of your private key serves to identify you. At the same time, you should not leak any information about your private key while using it to prevent a malicious party from learning your private key.
MPCitH
Multiparty computation (MPC) is a privacy-preserving technique that allows a group of entities to do a computation on their joint data without having a party reveal anything about their data except what can be derived from the computation’s outcome. For example, three hospitals may want to run a joint study on sensitive patient data which they are legally not allowed to reveal to each other. As long as the study outcomes do not allow us to derive anything about individual patients, MPC enables the hospitals to do the study.
A remarkable observation made in 2007 is that MPC can be used to construct ZKP’s by simulating a multi-party computation in the head (i.e. on one larger party!). In this case, a single instance runs the whole MPC computation. The actual proof mostly consists of publishing the information of some of the simulated parties in response to a request by the verifier. This allows us to verify that these parties did not misbehave. Intuitively, because in MPC no party should be able to learn anything about the data of any other party, this information does not leak anything about the undisclosed parties’ information.
We are interested in ZKPs which show that the prover knows $x$ such that $f(x)=y$ holds for a one-way function $f$ which is hard to invert, i.e., computing $x$ given only $y$, is intractable. For this, the prover can split $x$ into $N$ shares such that $x$ can only be recovered from all $N$ shares but $N-1$ shares leak no information about $x$ (this is called a secret sharing scheme). The prover then runs an MPC computation of the function $f$ on the secret shared content (i.e., $x$). Clearly, an honest execution of this protocol will result in $y$. A prover who does not know a valid $x$ can still try to simulate the MPC computation. However, in this case they must alter the behavior of one of the parties. This alteration is known as cheating, and the cheat must be performed right at the outset, before the verifier decides which parties they are going to inspect.
The bottleneck
Let’s say we run the above protocol for a one-way function $f$ and simulate $N$ parties. A verifier then needs to check that the prover hasn’t cheated. So the prover ‘opens’ all-but-one parties, leaving 1 hidden (selected by the verifier), which they could have cheated on. The verifier checks the prover’s computations in the $N-1$ parties, and so the prover has a $1/N$ chance of successfully cheating. To make this scheme secure, we commonly aim for a cheating probability of $2^{-128}$.
One way to get there is to make $N = 2^{128}$. However, this would require an honest prover to run on the order of $2^{128}$ operations, which is infeasible (the very reason we aim for the $2^{-128}$). Alternatively, we can repeat the same protocol for a smaller $N$ many times independently. Then the chances of the prover cheating successfully become $(1/N)^t$. Hence, any combination of $N$ and $t$ such that $t\log N = 128$ (for example, $N = 4$ and $t = 64$) will work.
However, for each independent run there is a large ‘offset’ which makes the data to be communicated large, and this offset is the same size whether $N=2$ or $N=1000$. This data later becomes the signature. So there is a trade-off: The larger we pick $N$ the smaller the signatures get. However, to decrease the signature size by a factor $k$ we have to increase $N$ (and thereby the computational costs) exponentially to $N^k$. Continuing the example above, starting from $N= 4$ and $t = 64$, if we want to halve the signature size ($t=32$) we would have to increase $N$ to $4^2 = 16$ which means a factor 4 increase in computation. If we aimed for a quarter of the signature size ($t = 16$) , we would have to go to $4^4 = 256$, meaning a factor 64 increase in computational cost.
While we can use the trade-off to reach extremely small signatures as well as extremely fast ones, we never get both at the same time. An important reason for this is the large offset per protocol run.
Our solution: aggregate…
We first observed that the operations of the MPC computation as well as those of the secret sharing scheme used in this scheme were linear, meaning they commute. That means that if you start with $N$ parties, combine the shares of two parties, then perform the relevant computations with the $N-1$ you are left with, you will get the same result as if you performed the computations on the shares of all $N$ and then recombined the results at the end. Our new idea is to start with $N$ parties as in the original scheme which we call “base parties”, but then perform a form of batch testing (see comparison at the end of the post!): we partition the parties into $M$ different sets and aggregate within each set to obtain $M$ new effective parties, which we call “main parties”. Then we run the MPC protocol with these main parties. This is repeated with different partitionings.
…on a hypercube! …
The partitions are selected to provide optimal coverage, i.e., after running the protocol for all partitions, all but a single base party should have been revealed to the verifier. The approach we took for this is to use a hypercube. This is best explained via visualization. Try drawing a 3x3 grid and arranging the base party shares on it. We have 9 shares, and first we’ll aggregate on the columns to create a 3-party protocol where each party’s shares are the sum of three base parties. And then perform the exact same process, but aggregating along the rows this time.
In this sense, we have two 3-party protocols, instead of one 9-party protocol, achieved by arranging the base parties on a square, or 2D cube. In the diagram shown, the prover can still only cheat with probability 1/9, by randomly selecting base party l2 and hoping that the verifier later selects the two parties that leave l2 hidden.
In fact this technique can be generalized to many dimensions, meaning we arrange shares on a multi-dimensional hypercube. We found the most efficient way to scale this is to pick the side of the cube to be 2 (versus 3 in our illustrative example), and then we generate $N=2^D$ base parties, where $D$ is the dimension of the hypercube. Now we perform one 2-party protocol for each of the $D$ dimensions, meaning we have 2D computations instead of $2^D$, in the original scheme.
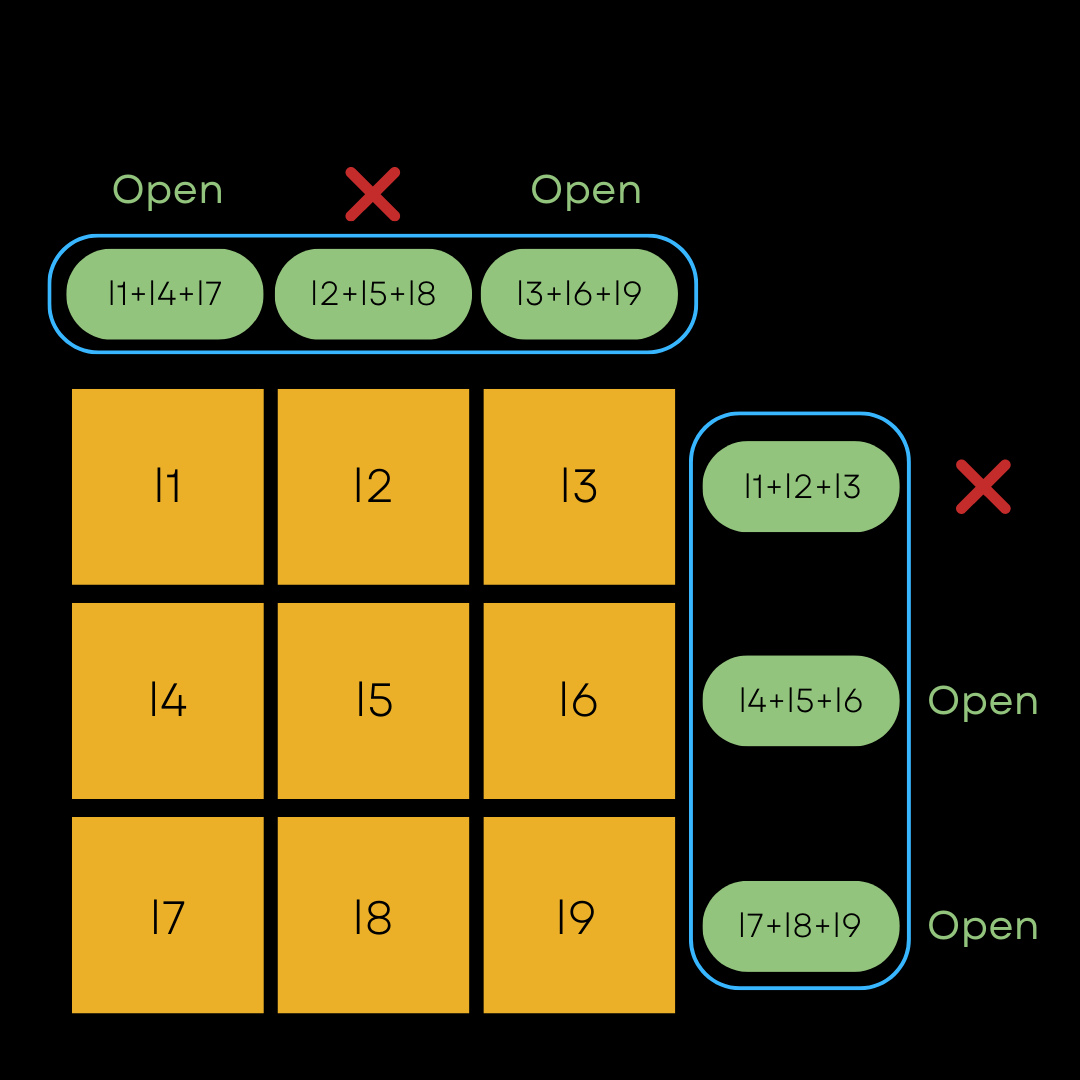
Base parties aggregated for MPCitH in two dimensions
[Bonus interlude - hypercube coronavirus tests!]
This technique of aggregate testing can be applied across many disciplines. In a paper published in Nature in 2021, a method for faster COVID-19 testing was proposed based on a very similar hypercube structure. The insight lies in that, if one sample contains COVID-19, then by mixing it with other samples, that aggregated sample will also test positive. The corollary is that individual tests do not have to be performed, which would take a long time and many resources during a period of great stress, but instead the coordinates of a positive aggregated hypercube test can be used to pinpoint the offending sample. The difference between this and the technique we have presented, is that the hypercube representation means that by performing the tests on aggregated hypercube samples, the only way to have cheated is by picking the correct coordinate to cheat on (l2 in our example) with probability 1/9 even though many fewer tests/computations are performed.
…to get faster/smaller signatures
The reduction in computation means we can use many more base parties in a single iteration of the protocol at the same cost, allowing to use a greater $N$. Consequently we need fewer repetitions $t$ such that $(1/N)^t$ reaches an acceptable security level. Each repetition requires a new offset, hence by using this trade-off we can get smaller signatures.
Here are some results using the hypercube compared to a very similar scheme that preceded the hypercube method:
| Scheme | Size (bytes) | (Base) parties | Repetitions $t$ | Sign time (ms) |
|---|---|---|---|---|
| Fast | 12,115 | 32 | 27 | 6.0 |
| Short | 8,481 | 256 | 17 | 23.6 |
| Shorter | 6,784 | $2^{12}$ | 12 | 313.7 |
| Shortest | 5,689 | $2^{16}$ | 9 | N/A |
| H-Fast | 12,115 | 32 | 27 | 1.3 |
| H-Short | 8,481 | 256 | 17 | 2.9 |
| H-Shorter | 6,784 | $2^{12}$ | 12 | 26.4 |
| H-Shortest | 5,689 | $2^{16}$ | 9 | 320.7 |
In the table we see signature performance for SDitH, and for hypercube-SDitH, denoted ‘H-’. The shortest parameter set was not presented in the previous work due to the infeasibility of computation without the aid of the hypercube method.
We in fact believe that the hypercube-MPCitH technique can be utilized to improve performance of a range of cryptosystems, not just the scheme we directly improved, but demonstrating this remains as an exercise for the reader!
Note on (non) interactivity
In Zero Knowledge Proofs (ZKP) we discussed an interaction between prover and verifier, as though the protocol is a conversation. In the context of verifying identity, this is called an identity scheme. But a signature is slightly different, it is non-interactive. For this, the role of the verifier in selecting random challenges can be replaced by mathematical tools. This allows the prover to construct an entire ZKP of their identity in an offline manner. This transformation, known as the Fiat-Shamir transform, allows us to turn an interactive identity scheme into a non-interactive digital signature.
