When in ROM, do as the quantum attackers do: Part I

“A humorous cartoon-style depiction, inspired by Indian cartoonist R. K. Laxman, blending the Roman Empire with a clear quantum technology theme.” by DALL-E3.
The National Institute of Standards and Technology (NIST) has just released the first set of Federal Information Processing Standards (FIPS) for post-quantum cryptography (PQC). So institutions worldwide, ranging from large banks to government agencies, now have a “recipe” to implement these standards in order to safeguard their IT infrastructure against threats posed by large-scale quantum computers (learn more about how SandboxAQ contributed to this standardization process in our recent blogpost). Now taking a step back, how does NIST know that the above standards are indeed secure against quantum attacks of the future? Perhaps surprisingly, the short answer is: they don’t! Now before you start panicking, let us expand on what we mean by this.
Most cryptography that is currently deployed–e.g., in HTTPS or your favorite messaging app–relies on some assumptions. Namely, that certain mathematical problems are difficult to solve with a reasonable amount of computing power. Examples of such problems include factoring large integers (by large, think numbers with 300+ digits) and computing so-called discrete logarithms. However in 1994, Peter Shor–then a researcher at Bell Labs–published a breakthrough paper which showed that these problems were in-fact easy to solve on a quantum computer. In other words, attackers with access to (noise-tolerant and sufficiently powerful) quantum computing can essentially break the security of the Internet; this can include infecting your clients’ software updates with malware, or reading your private WhatsApp messages. This essentially gave birth to the area of PQC where people are researching cryptographic algorithms that rely on problems which are hard even for a quantum computer. (Yup, such problems do exist! As Martin Albrecht–a Principal Research Scientist at SandboxAQ–wisely put it: “…quantum computers are not faster, they are weirder.”) For example, the NIST PQC standards ML-KEM and ML-DSA rely on the quantum-hardness of certain computational problems in module lattices (the “ML” in their names refers to “Module Lattices”).
Let’s go back to our question of how NIST knows whether their chosen standards are secure against quantum attacks. These standards come with a “proof” of security. To understand what we mean by a “proof”, let’s focus on the NIST standards ML-KEM and ML-DSA for the moment. Their respective security proofs basically show the following: if we assume the above module lattice problems are hard for quantum computers, then breaking these standards is also hard for an attacker that uses quantum computers (the proof for the remaining standard SLH-DSA also shows something similar wherein we assume the quantum-hardness of a different problem). More specifically, they prove the contrapositive (also called a “reduction”) – if there exists a quantum attacker that successfully breaks either ML-KEM or ML-DSA, then using the same attacker, we can solve the underlying module lattice problem easily using a quantum computer. And when we claimed NIST doesn’t know if their standards are quantum secure, what we meant is that NIST cannot guarantee if the quantum-hardness assumption of the ML problems holds in the far future – i.e., they cannot guarantee that a future “Shor” does not make another breakthrough which solves these problems easily on a quantum computer. But at the same time, this assumption is not unreasonable. A lot of bright people in the quantum community have tried solving these lattice problems for decades; however, it doesn’t appear that we’re anywhere close to a solution (a recent paper did claim a quantum algorithm which solves a related lattice problem, but the result was later found to be incorrect).
So after reading all of this, you might be thinking: “Oh, you scared me unnecessarily! If the quantum-hardness of ML problems (and similar) is the only assumption I’m willing to make, then yeah, the NIST PQC standards are indeed secure against future quantum attackers 🙂”. Unfortunately, that’s not quite the case, and we did not tell you the whole story yet. That is, the quantum-hardness of lattice problems is not the only assumption we’d need to make, and there’s another–and arguably, nonsensical–assumption underlying the NIST standards.
Enter hash functions
Before we dive into this “weird” assumption, let’s first focus on some simpler primitives called hash functions. Roughly speaking, they are functions which “hash” down potentially long input strings to fixed-size short strings or “digests”. If you happen to work in IT, chances are you probably used these functions in a non-cryptographic context such as databases or filesystems. However in cryptography, hash functions are quite ubiquitous, and they can be found in various cryptographic algorithms and protocols. So it should come as no surprise that the NIST PQC standards also employ hash functions; in fact, the remaining standard we haven’t talked about much till now–i.e., SLH-DSA– is entirely based on hash functions (the “H” in “SLH” stands for “Hash-Based”)!
Now even though hash functions make life easy when designing cryptography, they often make things difficult when trying to provide a security proof/reduction (as described above) for the resulting schemes. It is usually the case that we need to make some non-standard assumptions about the underlying hash functions just for a security proof to go through; these assumptions are stronger than more common ones such as the hardness of finding preimages of hashes (i.e., preimage resistance) or finding collisions in hashes (i.e., collision resistance). In particular, what we require is that the hash outputs are perfectly “random”.
Why is this randomness assumption non-standard? According to information theory, for a hash function to produce perfectly random outputs, its description needs to be quite large (and the time it takes to compute hashes would be quite slow as a result). Compare this to a real-world hash function such as SHA3-256 used in the NIST standards where the algorithm description can be contained in a few hundred lines of code and where it only takes a few microseconds to compute hashes. In other words, SHA3-256 definitely does not satisfy this randomness assumption. But spoiler alert, the security proofs for the NIST PQC standards still make this assumption on their underlying SHA3-256 and similar hash functions…
You might now say: “Wait a minute. Then how are the security proofs for the NIST standards valid when the underlying “random hash” assumption is obviously false? What are the proofs even “proving” at this point? Does this mean the NIST standards are not secure against quantum attacks?”. Well first of all, please take a deep breath. Now these questions are perfectly reasonable to ask; in-fact, they have been plaguing the cryptographic community for years and are subject of a wider debate. However we won’t be covering these philosophical issues in this blogpost (but we do recommend checking out Matthew Green’s excellent blog series on the matter). This blogpost will instead be about how the security proofs–e.g., the ones for the NIST PQC standards–use this weird randomness assumption on hash functions at a technical level.
The random oracle model: theoretical cryptographers hate this one weird trick
Recall that a security proof for a cryptographic scheme generally shows the following – if there is an attacker which successfully breaks the scheme in question, then we can construct a reduction algorithm which solves the underlying assumed hard problem by using the above attacker. So in this setting, we broadly have three parties: the “attacker”, the “scheme” (e.g., ML-KEM) and the “algorithm” (e.g., to solve an ML problem) . Now let’s say the scheme makes use of a hash function like SHA3-256. Then it’s not hard to imagine that each of these parties also have local copies of the hash function with them, as the function is publicly available. However if we want to use the “random hash” assumption in our proof as well, then each of these local copies would be too huge to store because of their large descriptions mentioned above (as implied by information theory) and would be painfully slow. So how can we salvage the proof in this situation?
In 1993, Mihir Bellare and Phillip Rogaway–then researchers at IBM–essentially proposed a “trick” in a seminal paper to make cryptographic security proofs compatible with the randomness assumption on hashes. More formally, they described a paradigm where instead of giving the above parties local copies of a concrete hash function, we provide them global access to an object called a “random oracle” (in IT networking terms, think of the “random oracle” as a global server which gives clients/users access to randomness); this paradigm is also popularly called the “random oracle model”, or ROM. Now whenever a party wants to compute a hash of a value, it would ask (or “query”) the random oracle on this value instead, and get back a response which is to be interpreted as the digest. To maintain sanity, this oracle would have the same input and output spaces as that of the replaced function (e.g., a random oracle replacing SHA3-256 would also output digests of length 256 bits), and would also be consistent across different parties (i.e., if the “attacker” and the “scheme” query the oracle on the same input, then they would get back the same output). More interestingly however, the oracle satisfies the randomness assumption too. That is, each unique input to the oracle would be mapped to a uniformly random and independent output.
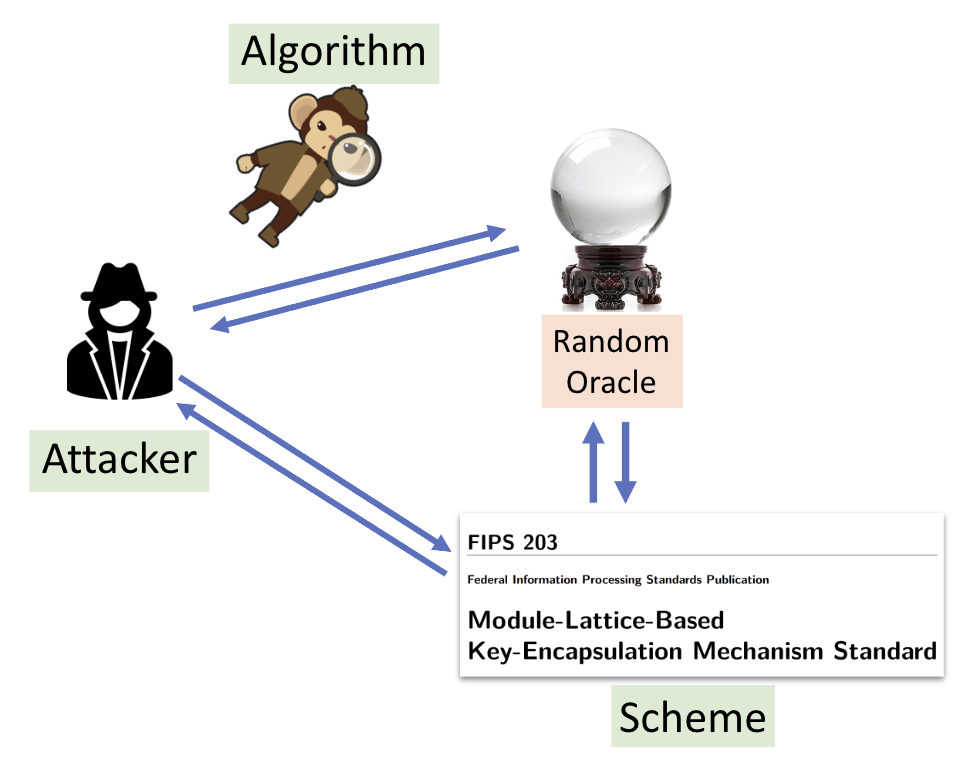
The “algorithm” observing the attacker’s queries to the random oracle/hash function in the ROM.
Let’s take a pause. All of this sounds crazy, right? But we’re not done yet – buckle up! When devising a security proof in the ROM, the “algorithm” is also allowed to observe the oracle/hash queries made by the attacker, is allowed to intercept the oracle responses and mess with them (also known as “programming the random oracle” in the literature), and generally is allowed to simulate the entire random oracle on its own towards the “attacker”! This of course does not reflect the real world where these “random oracles” in security proofs are instantiated with concrete hash functions like SHA3-256. For example, consider a scenario where an attacker, in their attempts to break one of the NIST PQC standards, evaluates the underlying SHA3-256 function locally; now such queries are clearly not public, and we cannot really “program” SHA3-256 because it is a public function. So with these discrepancies in mind, such security proofs in the ROM should be thought of as “heuristics” at best. But nevertheless, …
… a ROM proof still provides a good heuristic in the sense that it precludes obvious weaknesses in a cryptographic scheme – in other words, if there is a practical vulnerability in such a scheme, then the reason does not lie with how the scheme is using the underlying hash function, but it has to do with problems related to the hash function itself.
Now to the valiant readers who have made it this far and still have a nagging feeling that there’s something wrong with the ROM but can’t quite put their finger on it, look no further! A 1998 paper showed the existence of schemes that have a security proof in the ROM but are nevertheless completely insecure when the random oracles are instantiated with any concrete hash function. These schemes however are quite “artificial” and most likely won’t be used in practice (or at-least we hope!); for example, some of these schemes output the secret key if a certain trigger condition holds. But in essence, the above result shows that ROM security proofs need to be taken with a significantly large grain of salt.
Despite this shortcoming of the ROM, the paradigm has found widespread usage in the real world because it allows to prove security of cryptographic schemes (albeit heuristic) that are quite efficient in practice. In contrast, schemes that do not rely on random oracles for their provable security often have a worse performance compared to their ROM counterparts. Hence, the ROM became one of those things where cryptographers can’t live with them, can’t live without them…
The random oracle model (Taylor’s quantum version)
Up until now, we have only been focusing on the classical–or so called, “pre-quantum”–setting. But a careful reader might note that the title of this blogpost alludes to quantum attackers. So let’s picture such a quantum attacker who wants to break the NIST PQC standards. Since we’re in a “post-quantum” setting, we assume the attacker has a sufficiently powerful quantum computer at their disposal. Now consider the SHA3-256 hash function underlying the NIST standards. A useful fact about quantum computing is that any function that can be implemented on a conventional computer can also be implemented on a quantum computer. So it’s not hard to imagine that our quantum attacker can implement the public SHA3-256 function on their quantum computer. This would allow the attacker to evaluate SHA3-256 hashes in a quantum superposition, which in turn could assist their attack against the NIST PQC standards (e.g., the attacker can find SHA3-256 collisions faster this way when compared to the classical setting). So how is this scenario reflected in the ROM above, when SHA3-256 is modeled as a random oracle?
Unfortunately, in Bellare and Rogaway’s original description of the ROM, all parties–including the “attacker”–technically only have classical access to random oracles. In other words, the model is insufficient to capture the above quantum attack. Hence to account for such scenarios in a post-quantum setting, a 2011 paper proposed to “patch” the classical ROM such that the “attackers” in security proofs can now have quantum access to the random oracles; perhaps unsurprisingly, the new model was simply called the “quantum random oracle model”, or QROM. This enhanced security model in turn proved to be quite important as subsequent work has shown that there do exist post-quantum cryptographic schemes which can be shown to be secure in the classical ROM but which are completely insecure in the QROM. As a result, QROM became a go-to model to analyze real-world cryptographic schemes in a post-quantum setting – for example, NIST recognized the QROM when vetting submissions to its PQC standardization process.
Now the above post-quantum patch to the ROM might look simple, right? However, this seemingly small change opens a Pandora box of challenges for translating ROM security proofs to the QROM. In our next blogpost of this series, we will explain how cryptographers managed to salvage this situation in the QROM. We’ll specifically focus on some novel techniques that researchers–including those in SandboxAQ’s Cybersecurity group–introduced in the QROM setting, which allowed us to prove post-quantum security of important cryptographic schemes such as the NIST PQC standards.
