Lighting the Signal

“drawing of a female scientist breaking code by lighting the signal as Van Gogh” by DALL-E.
Key exchange is one of the fundamental building blocks that Internet security is built upon. The goal of key exchange is for two parties – often called Alice and Bob – to do computations such that at the end they agree on a shared secret key. This key is then used to encrypt messages using symmetric encryption. In this post we will explain the core idea behind a recently published attack against one kind of key exchange protocol. Specifically, we will discuss “signal leakage attacks” against key exchange protocols, which are based on the Learning with Errors (LWE) problem under “key re-use”.
The respective paper “Light the Signal: Optimization of Signal Leakage Attacks against LWE-Based Key Exchange” by Yue Qin, Ruoyu Ding, Chi Cheng, Nina Bindel, Yanbin Pan, and Jintai Ding has been accepted at ESORICS 2022 (September 26-30, 2022, Copenhagen, Denmark) and will be presented virtually on Monday, September 26. The paper can be accessed on IACR eprint 2022/131.
One of the earliest and arguably simplest key exchange protocols was designed by Diffie, Hellmann, and (in an independent work) Merkle in 1976. The idea is that Alice and Bob each choose secrets $s_A$ and $s_B$, respectively. For simplicity it is sufficient to think of these elements as integers although they are actually ‘group elements’ in a group ‘generated’ by an element $g$. Then they transmit g raised to the power of the respective secrets to each other. These transmitted public values are known as $p_A$ and $p_B$. The shared secret key is then computed by taking the received public value again to the power of their own secrets. The security of this protocol is based on the discrete logarithm problem. That means, although the values $g$, $p_A$ and $p_B$ are publicly known, it is not possible to compute $s_A$ or $s_B$ from them. While this is true for our current computers, large fault-tolerant quantum computers will be able to solve the discrete logarithm problem, thereby breaking the security of the Diffie-Hellmann-Merkle key exchange and many other of today’s cryptographic algorithms (visit our blog post for more information about the quantum threat and actions to maintain security in the quantum era).
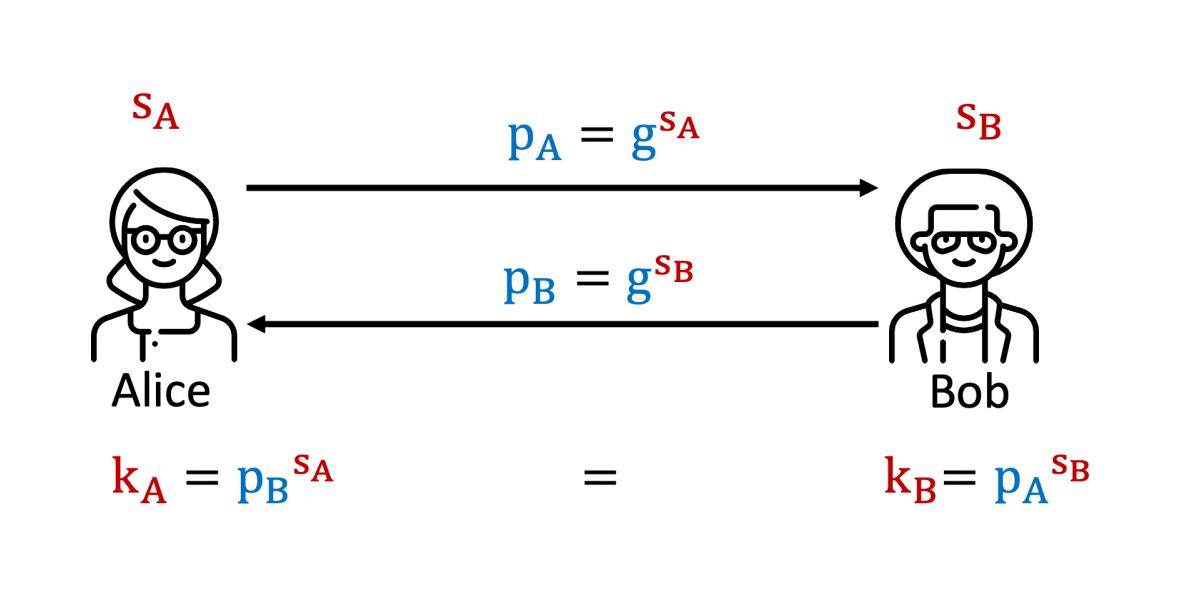
Simplified Diffie-Hellmann key exchange protocol with group generator g; secret values are red, public values are blue.
Alternative protocols that share many similarities are key exchange protocols based on the so-called Learning with Errors problem. As before, Alice and Bob choose secrets. This time the secrets are polynomials with small coefficients, e.g., $s_B = 1+2x-3x^2-x^{213}+4x^{317}-3x^{511}$. Using a publicly-known polynomial $a$ (similar to the element $g$ above) and their respective secrets, they compute public values $p_A$ and $p_B$ and send them to each other. They are then able to compute values $h_A$ and $h_B$ which are ‘approximately’ the same. To be able to compute ’exactly’ the same secret key, Bob needs to send additional information. This information is called the signal $w_B$. The signal consists of a list of zeros and ones – as many as the secret has polynomial coefficients. It can be used, together with $h_A$ or $h_B$, within a function $\text{Key}_F$ that outputs the final key.
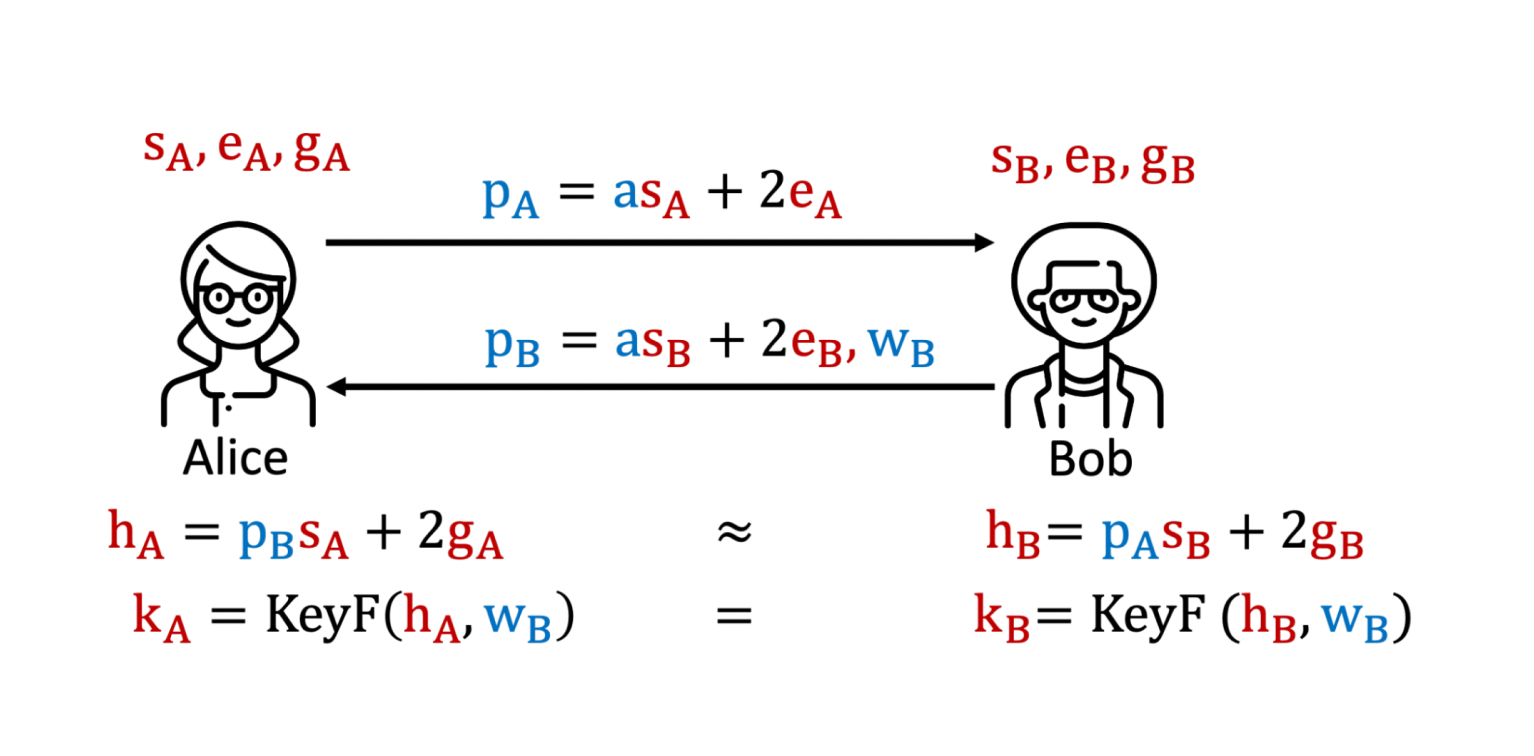
Simplified key exchange over the learning with errors problem with publicly known polynomial $a$
Unfortunately, this extra information allows for attacks to recover Bob’s secret $s_B$ if Bob does not change his secret ’every’ time, i.e., when he ’re-uses’ his secret. This kind of attack is called ‘signal leakage attack under key re-use’ and was first described by Fluhrer and later carried out against the LWE-based DXL key exchange by Ding, Xie, and Lin. The idea is that an adversary pretending to be an honest user sends malformed $p_A$. In particular, instead of a polynomial, the adversary sends $q$ different integers, namely $p_A=0, p_A=1, \dots, p_A=q-1$ for some system parameter $q$. By construction of the signal, it turns out that each element of the signal “flips” between zero and one twice as often as the absolute value of the corresponding secret coefficient. So by tracking the behavior of the signal as $p_A$ varies, the adversary can learn about the secret.
Let’s take a look at an example. Assume the adversary wants to find out the third coefficient of the secret polynomial $s_B = 1+2x-3x^2-x^{213}+4x^{317}-3x^{511}$ from above. To do this, the adversary sends $p_A=0$ to Bob, and stores the third value of the signal, which corresponds to the signal for the third polynomial coefficient. Looking at the diagram below, we can see that this signal value is equal to zero. Then the adversary sends $p_A=1$, and again stores the third signal value, which is again equal to zero. As visualized in the diagram, the signal value changes from zero to one for the first time for a value around $p_A=1800$, and back for $p_A=4000$. Increasing $p_A$ further until $p_A=16384$ leads to six ‘main’ switches. Therefore, the absolute value of Bob’s corresponding third secret coefficient is equal to 3. The adversary has to do this procedure for ‘all’ polynomial coefficients, which are usually 512 or 1024. In addition, the adversary needs to do a similar procedure to find out the sign of the secret coefficient (e.g., in the example above the secret coefficient is -3).
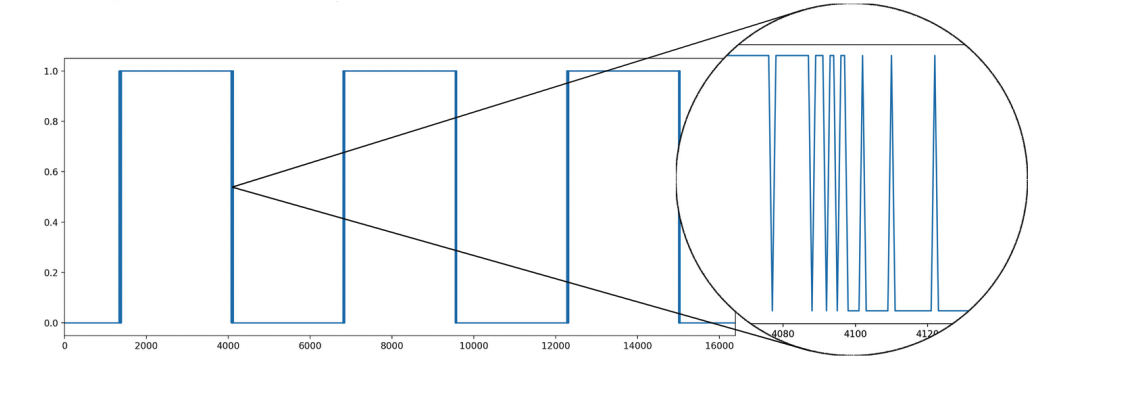
Example of signal switch for $p_A=k=0,…,16384$; source: Fig. 3 of IACR eprint 2020/1288
Zooming into one of the switches reveals that for a few values the signal actually fluctuates. This is caused by the random element $e_B$. Based on this, one can distinguish between ‘stable’ (blue or yellow in the figure below) and ‘unstable’ (wavy white) regions. To count the number of stable and unstable regions correctly, and as such to be able to count the number of ‘main switches’ correctly, it is not necessary to request $q$ different values for $p_A$. Instead Bindel, Stebila and Veitch show that it suffices to make sure to choose at least one value in each stable and at most one value for each unstable region for every possible absolute secret value. For example in the picture below, assuming that the absolute value of the secret coefficient is at most 3, the green values for $p_A=k_i$ are sufficient to determine whether the secret coefficient is equal to 1, 2 or 3. This way, it was possible to reduce the number of needed values for $p_A$ from a total of 98310 to only 1266 to recover the secret used in the DXL key exchange.
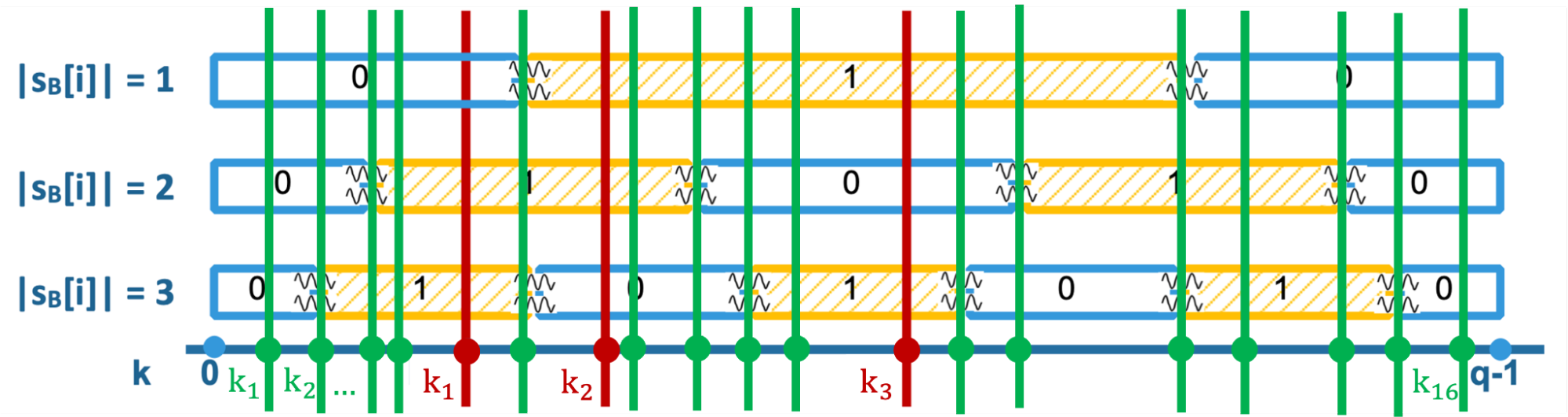
Comparison of values $p_A=k$ in the work by Bindel-Stebila-Veitch (in green) and the recent improvement (in red); based on Fig. 2 of IACR eprint 2022/131
Recently, Qin, Ding, Cheng, Bindel, Pan, and Ding were able to reduce this number further to only 29 values! The idea for this latest improvement is to choose the values even more cleverly. As can be seen in the above figure, actually the three red values are sufficient to uniquely identify the absolute value of the secret coefficient. The idea is to determine codewords that uniquely correspond to possible absolute values. For example, if the code word is $k_1-k_2-k_3 = 0-1-1$, the absolute secret value is equal to 1. And if the code word is $1-1-0$ or $1-0-1$, we know the absolute secret is 2 or 3, respectively.
This new interpretation of the signal leakage not only reduces the number of required values (therefore making the attack more efficient and more practical), but it also makes it easier to discover whether schemes can be broken by this kind of attack.
Lastly, it is important to mention that signal leakage attacks can be prevented using generic constructions of ‘authenticated’ key exchange protocols. It is, however, desirable to instead construct key exchange directly from a hard problem such as the Learning with Errors problem, e.g., to achieve better efficiency. Therefore, building such ‘direct’ authenticated key exchange protocols is attempted and failed regularly. The new improvements on the signal leakage attacks caution once more against underestimating the power of signal leakage attacks when attempting such constructions.
